By

文章目录
  1. 1. VC Bound
    1. 1.1. 证明
    2. 1.2. 计算VC
  2. 2. VC Dimension
    1. 2.1. 定义
    2. 2.2. 物理意义
    3. 2.3. 模型复杂度
    4. 2.4. 采样复杂度
  3. 3. 参考

VC Bound

我们通过上一篇文章中了解到了break point以及Growth Function之后，
我们将Growth Function的上界设为B(N,k)（maximum possible m_H(N) when break point = k），表示在break point的k的情况下，其mH(N)的最大值，用通俗的话来说，在N个点中，任意取k个点不能shatter。

这种方式定义的好处就是以后在计算不需要计较具体的成长函数是怎么样的，形成的hypothesis究竟是如何的。

证明

那能否证明B(N,k)<=ploy(N)呢？
先来看下面这个表,其中当前纵向有N，横向表示具体的k值，表中的内容就是需要计算的B(N,k)值

  • B(2,2)=3，B(3,2)=4 手算-_-

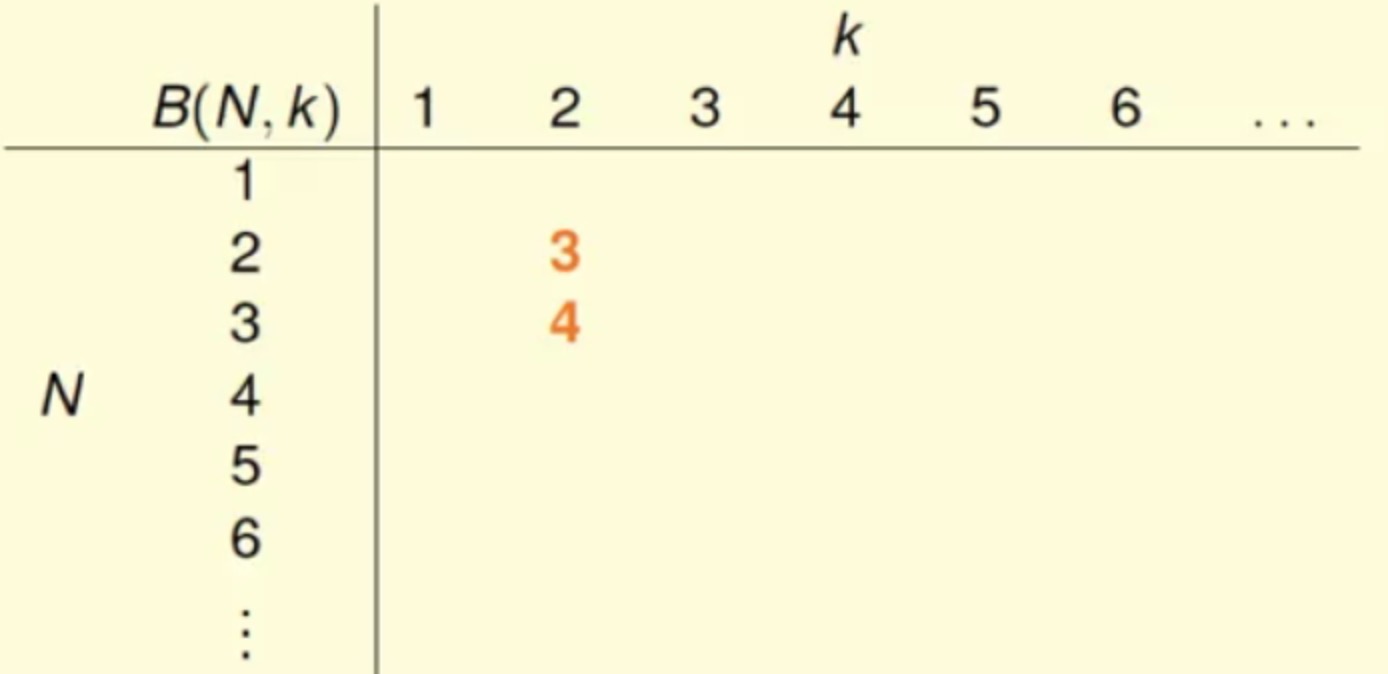
    因为任意两个点都不能被shatter，那么2个点产生的dichotomies不能超过3,同理3个点产生的dichotomies不能超过4

  • B(N,1)=1

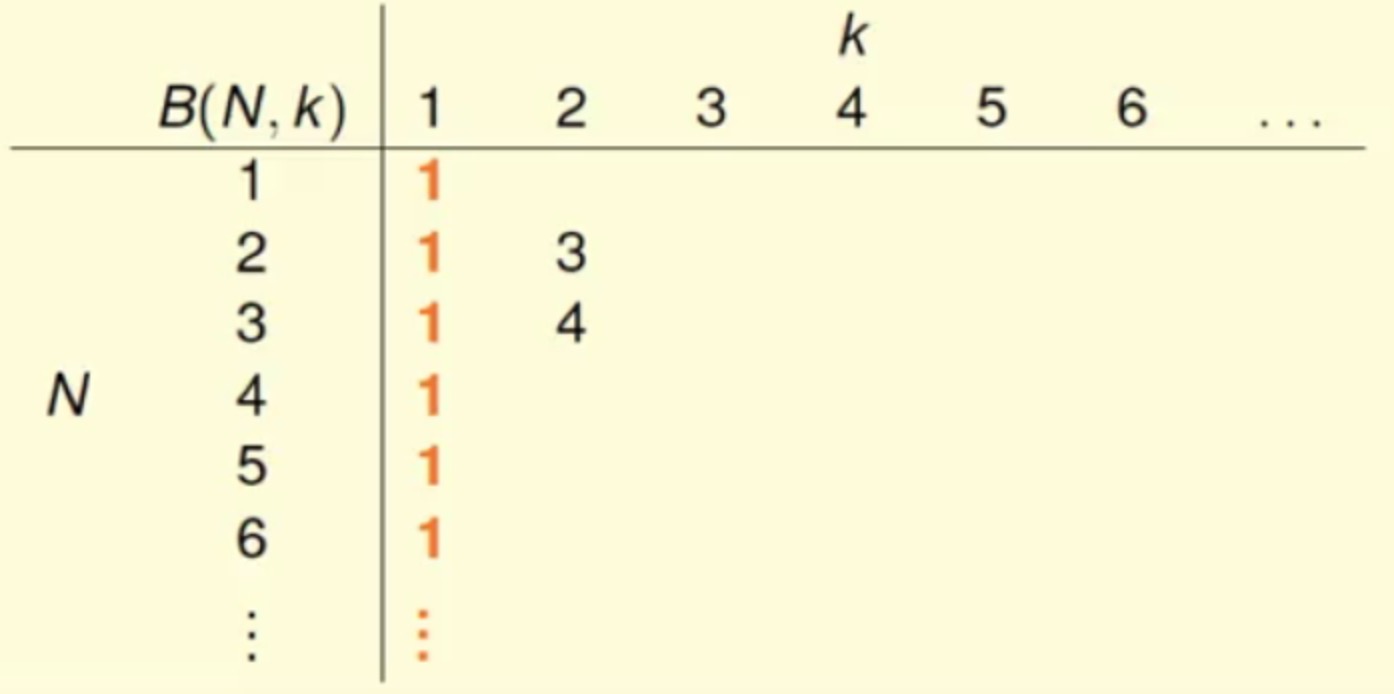
    2^1=2 而最大值不能超过2，所以这里最大值都为1

  • B(N,k)=2N 当N<k

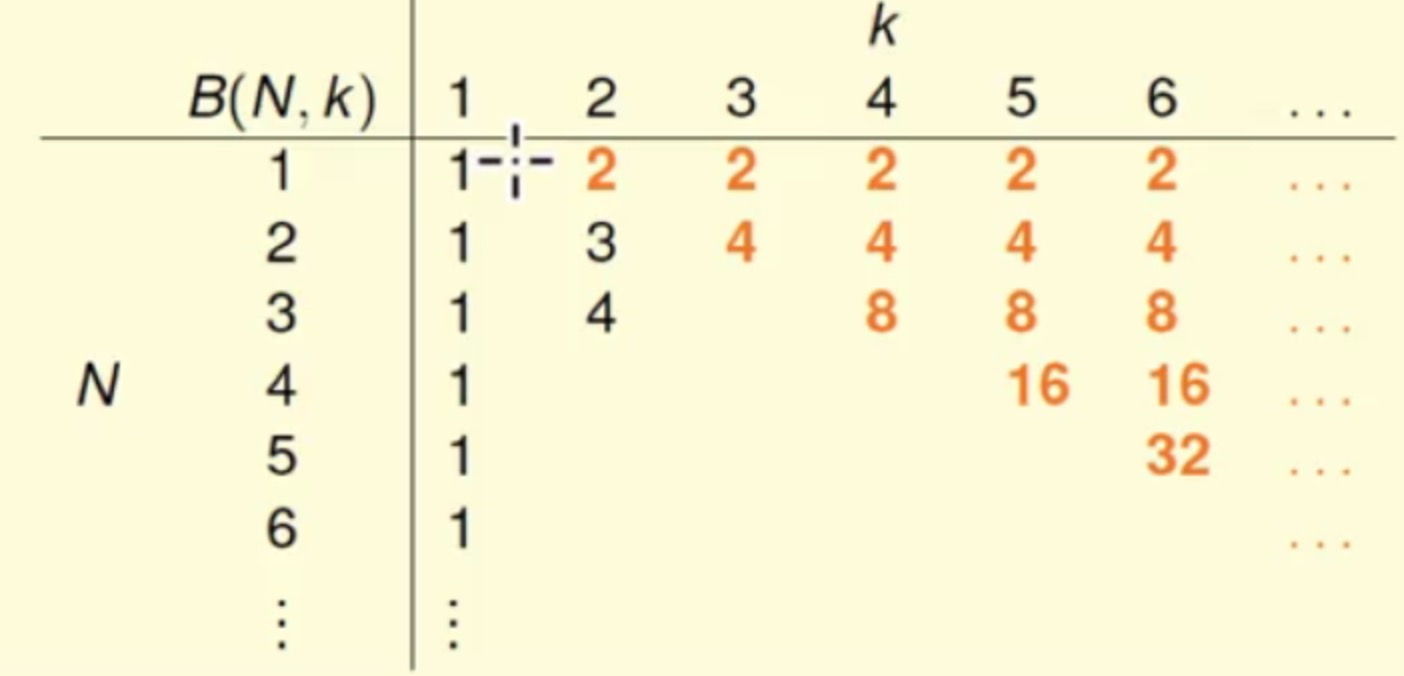
    这里的2N<2k必然成立，所以最大值直接取2N，不然多余选的点也都是重复的。

  • B(N,k)=2N-1 当N=k

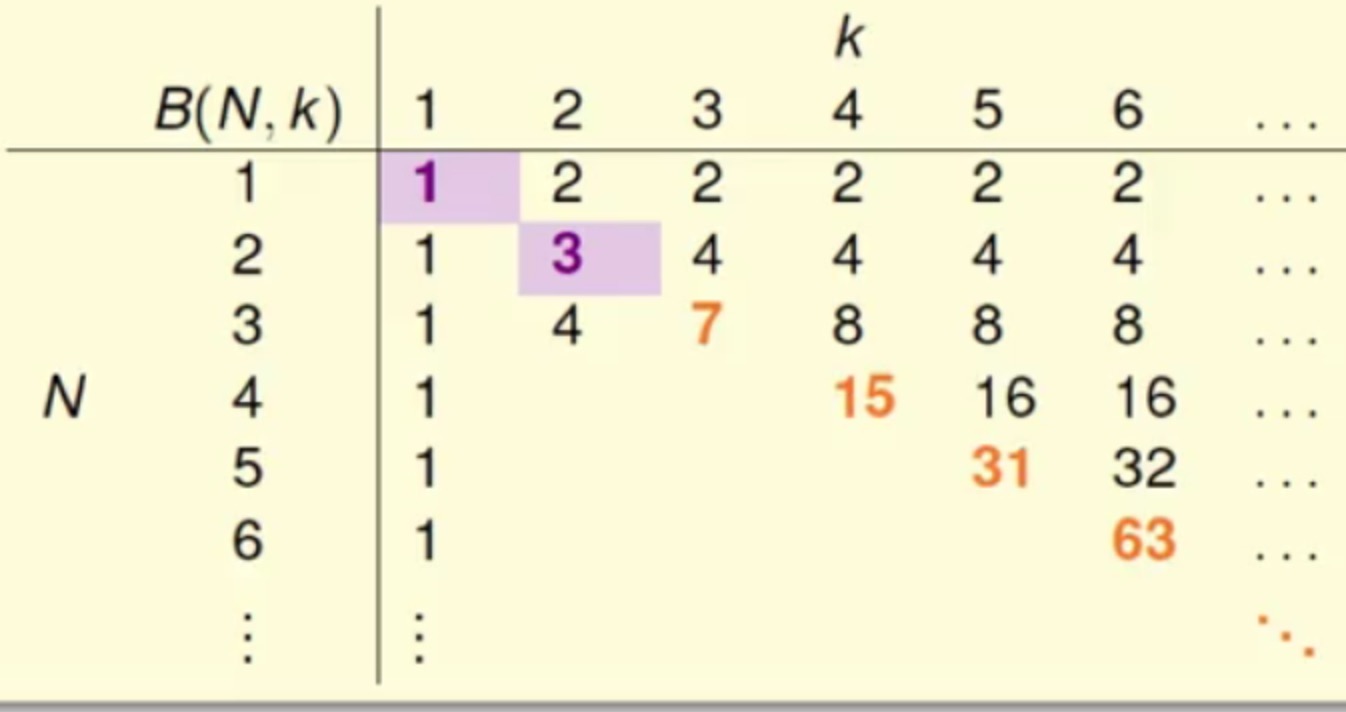
    在N=k的情况下满足全部不可能（点的所有组合为不可能），但是这里再减去一种就可以满足了

  • B(N,k)<=B(N-1,k)+B(N-1,k-1) 当N>k

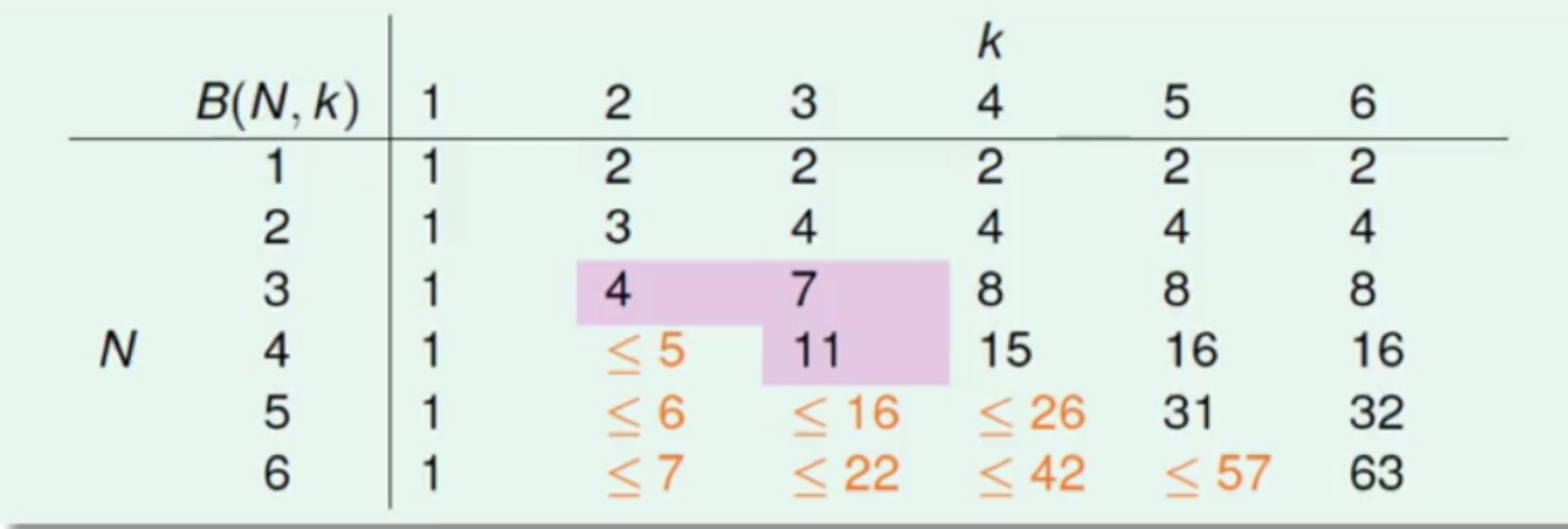
    表中新添的值为上限的上限，耐心地看下上图的推导-_-

    1. 通过计算机暴力求解B(4,3)=11,(一共16种dichotomies,再从其中选不同情况的dichotomies来计算是否被shatter，最终有216情况)

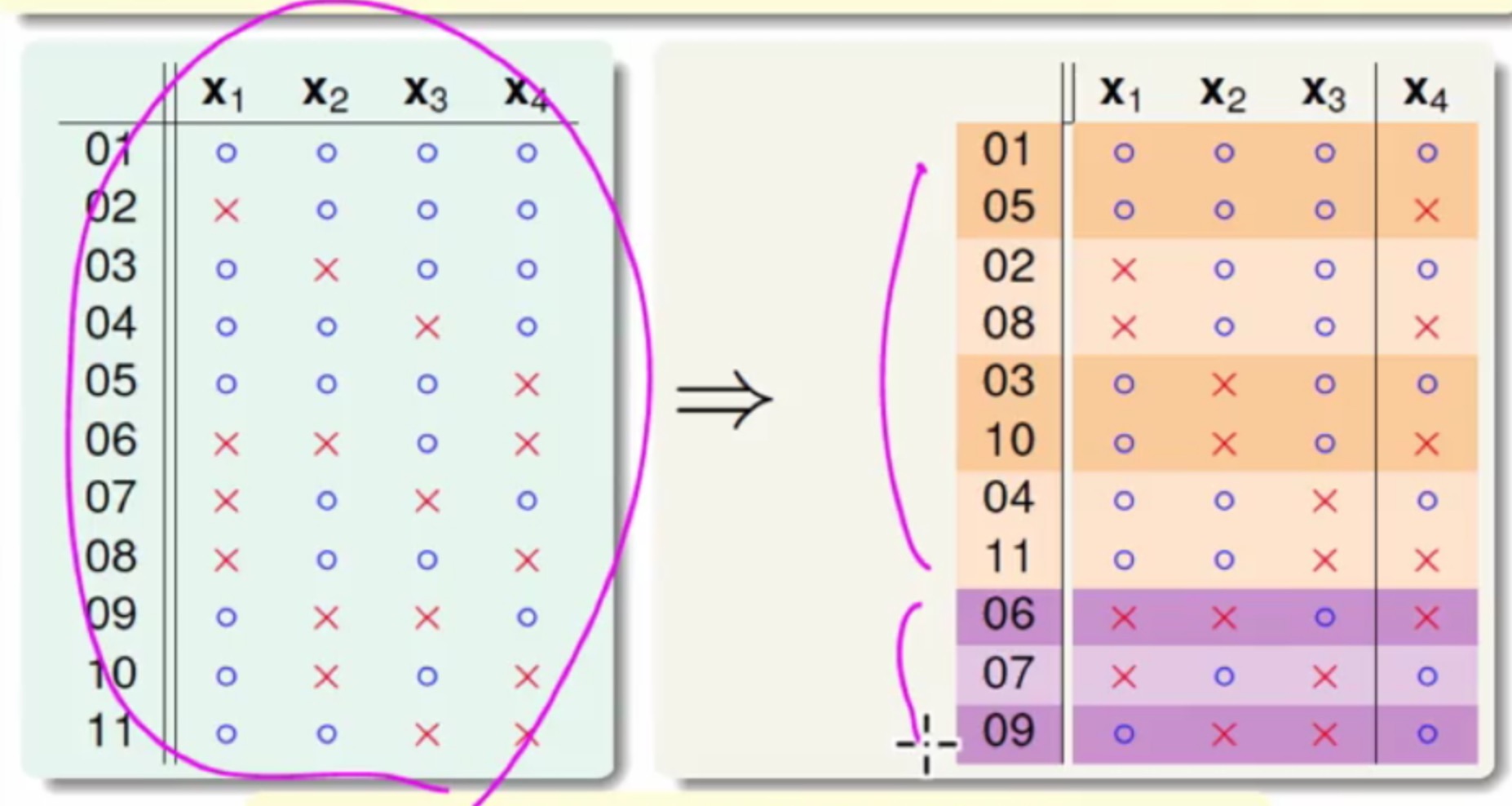
      右侧着色的图中橙色的点在x1,x2,x3这三个维度是一样的，x4这个维度是不一样的（也就是传说中的成双成对），蓝色的点在x1,x2,x3无法找到全部一样的
    2. 现在将x4这个点遮掉
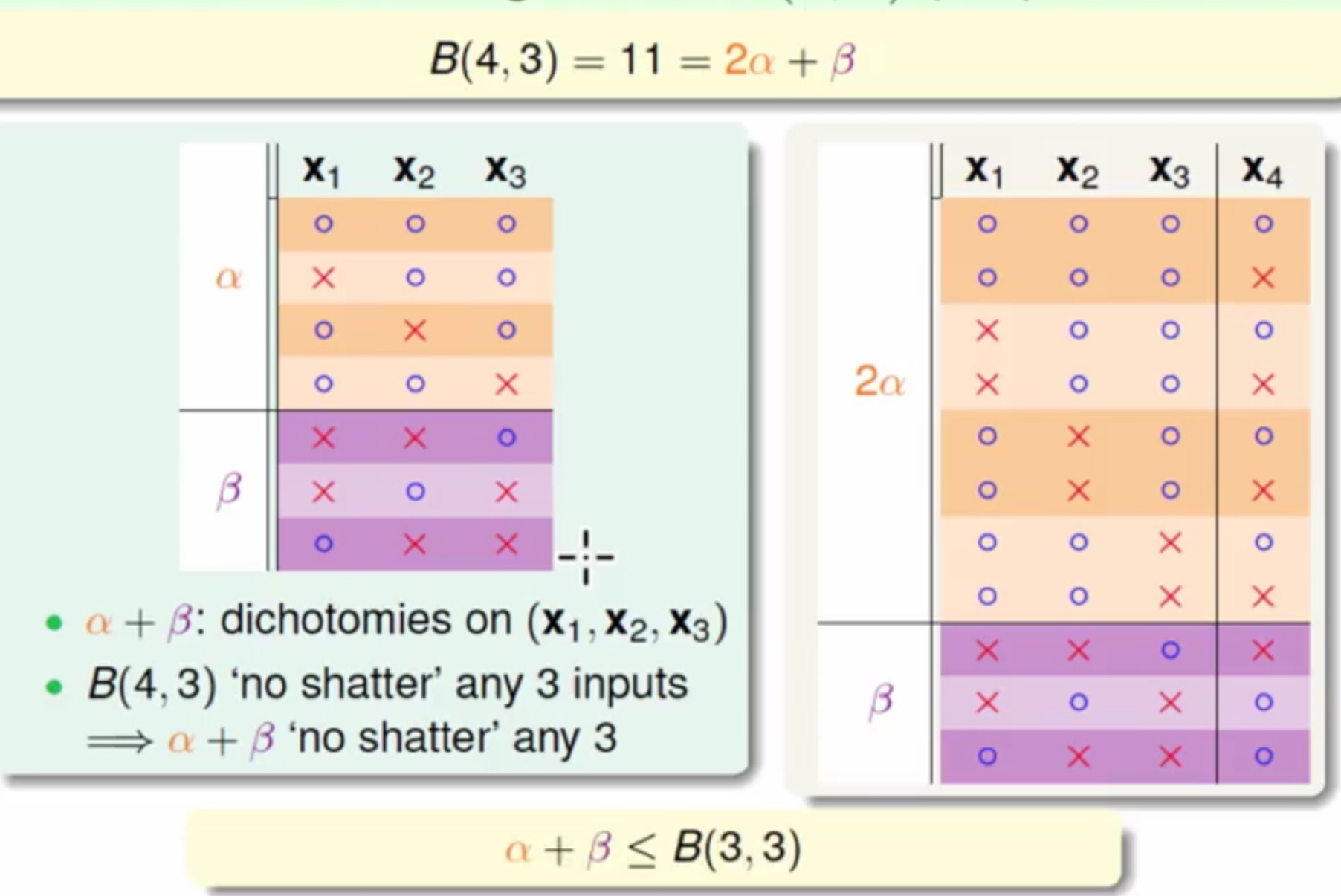
    3. 同时将蓝色的遮掉

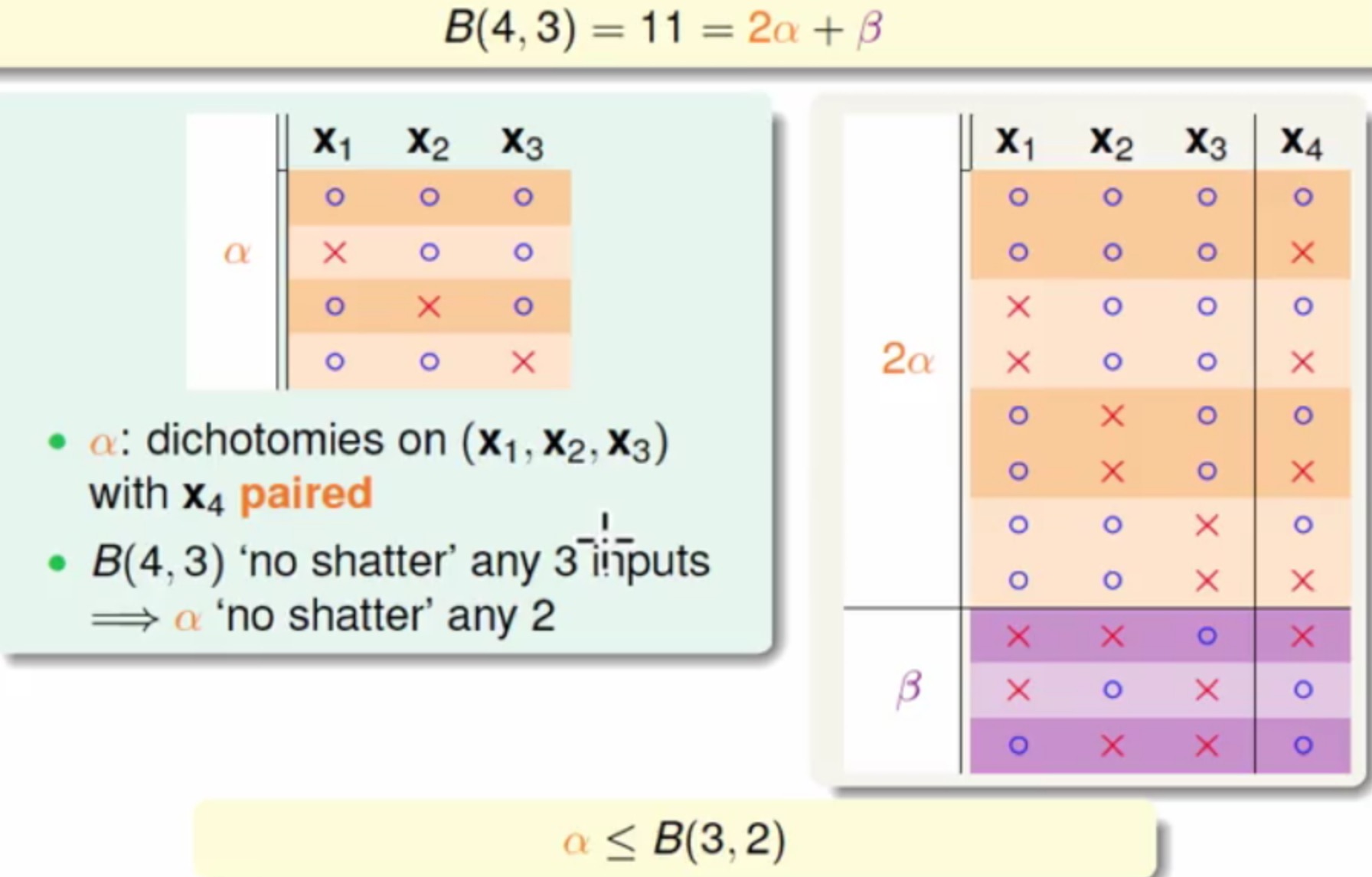
      这里不能多余2个点被shatter
    4. 整理之后就可以得到如下关系式
    5. 写成通用式子为

      即得解^_^

根据上限的上限的递推式，再结合数学归纳法可以得到

它的最高项的指数是k-1

那么现在：

  1. Growth Function会被上限B(N,k) bound住
  2. 而B(N,k) 又会被上限的上限bound住
  3. 这个上限的上限的多项式和break point点有关
  4. 所以可以得出结果，只要break point点存在，那么他的Growth Function最终会是一个多项式

但是然并卵，mH(N)并无法直接代入到之前的

计算VC

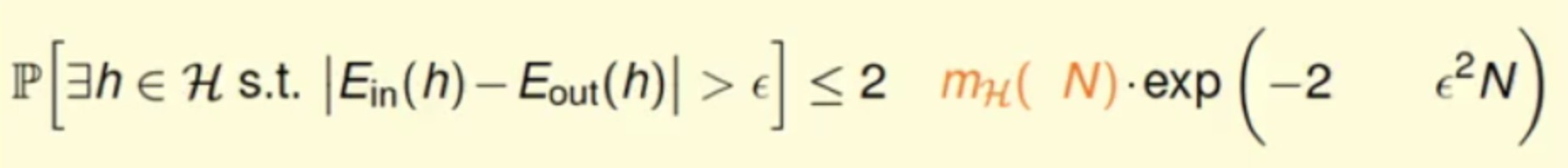
主要是因为：Ein(h)的hypothesis可能取值是有限个的，但Eout(h)的可能取值是无限的。可以通过将Eout(h) 替换为验证集(verification set) 的Ein‘来解决这个问题。

好，那么接下来主要经历如下三个步骤：

  1. 使用Ein‘来代替Eout
  2. 这样最终可能出现的H(x1,x2..xn,x1’,x2’…xn’)
  3. 使用不替换的Hoeffding

最终得到了著名的VC Bound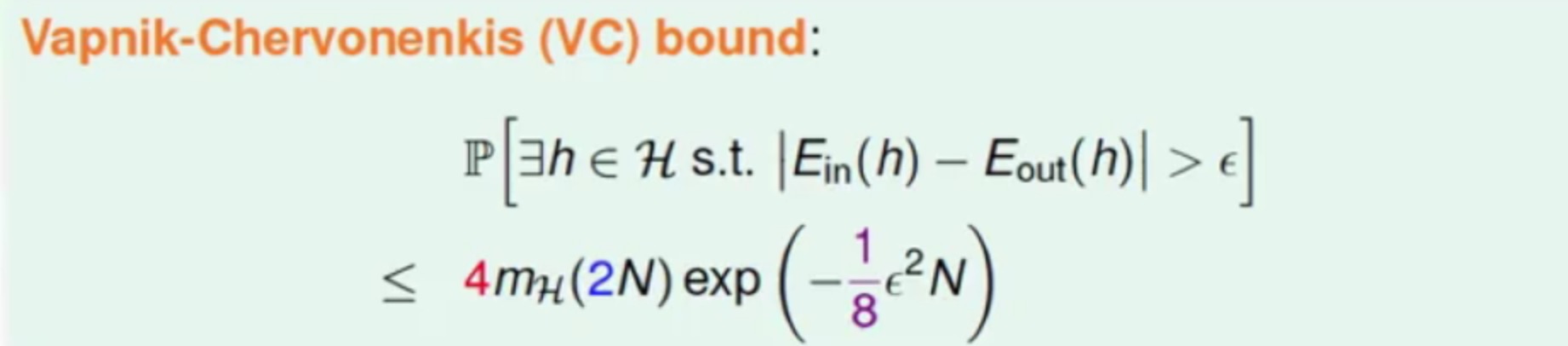

那么终于可以说明空间存在有限的break point，并且采样的资料量N够多，就可以保证找到一个Ein(h)最小的时候，得到最小的Eout(h),也就是说明Learning的可行性

VC Dimension

定义

先来看一下VC Dimension的定义

VC Dimension表示在N个点中能够shatter的最大的值，也就是k-1（k为break point,该值时不能shatter的最小值）

这样的话就可以很容易计算出我们之前一直在讨论的那几种情况的VC Dimension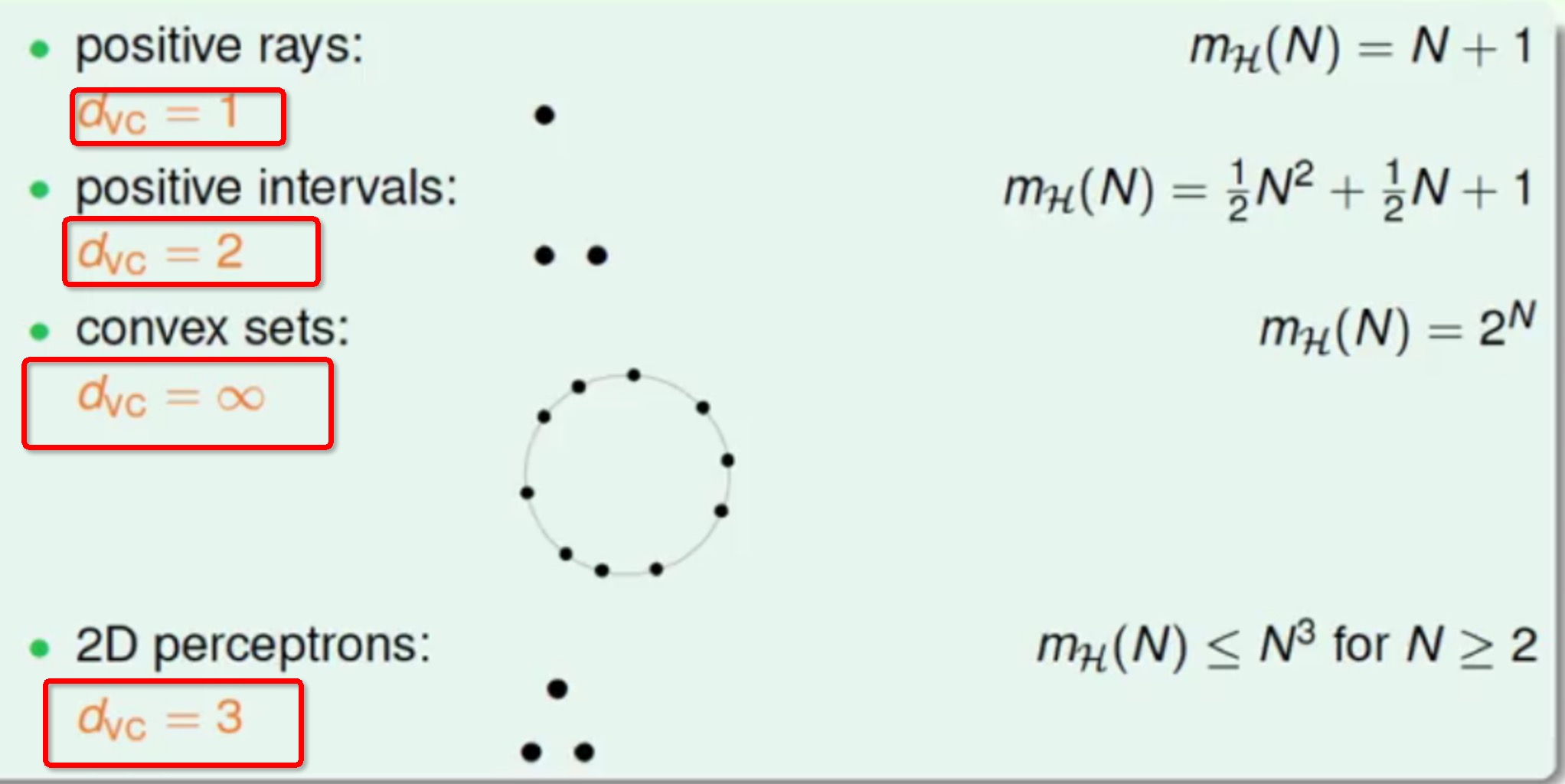

那么我们可以知道好的VC Dimension应该是有限的，这样才可以保证Ein≈Eout
同时这样就就会有

  1. VC Dimension与算法A无关
  2. VC Dimension与数据p的分布无关
  3. VC Dimension与目标函数f无关

说了这么多，看一下VC Dimension与大M的关系

这样就可以看到：

  1. M很小的时候，得到的Ein、Eout会非常相似，但是可选的Ein太少了，可能到最后选择了 一个较大的Ein
  2. M很大的时候，可选的Ein比较多，可能到最后得到的Ein得到的Ein、Eout可能不怎么想相似
  3. VC Dimension很小的时候，与第一条一样，但是区别的是它的自由度受到了限制
  4. VC Dimension很大的时候，与第二条一样，但是区别的是它的自由度没受限制，很自由

VC Dimension反映了假设空间hypothesis set的强大程度，VC Dimension越大，hypothesis set也越强，因为它可以shatter更多的点。

物理意义

VC Dimension的物理意义是表示二元分类下的自由度是多少，而这个自由度是表示参数w的维度

模型复杂度

现在将之前任意一hypothesis发生坏事的概率VC bound变一下形

最终，根号里面的叫做模型复杂度，模型的复杂度越大，其泛化能力就会越低，这个模型的复杂度越与三个项有关：

  1. N，抽样有多少个点
  2. H，这里的VC Dimension有多大
  3. δ，Ein与Eout相似在一个阈值内的概率

现在在图上画出三者的关系：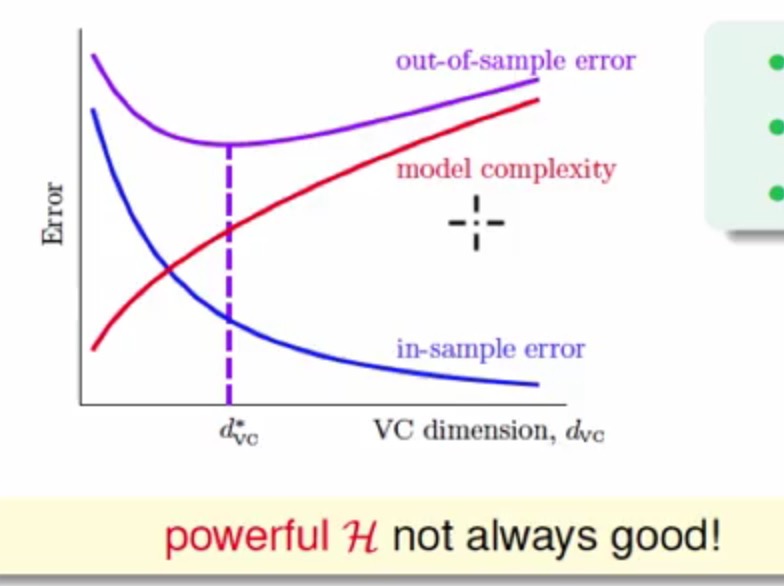

那么可以看到随着VC Dimension越大，其模型复杂度也会越大,Ein会变小，但是Eout会有像图中一样一个山谷形的表现，最小的Eout会在中间

所以更加深层次的可以了解到，我们并不是把Ein做的越小越好，因为这个时候可能会导致模型复杂度变大，从而最终使Eout也会变大,真正会做机器学习的人在优化Ein的同时会考虑带来的其他复杂度的代价。

采样复杂度

VC bound的另一个意义就是模型复杂度
那就现在给你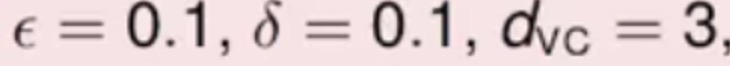

这些参数，那么如果计算使用最少的样本量来完成上述需求，计算过程可以参考下面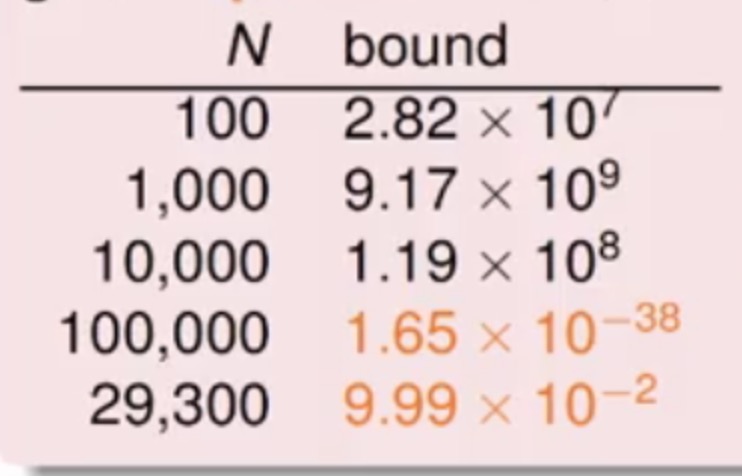

而在理论上需要的样本是N≈10000dvc
但是其实在实际上N≈10dvc即可,
为什么会这样呢？

这是因为VC bound推导的过程很宽松，里面很多假设都是取了上限

所以，模型较复杂时(N≈10dvc 较大)，需要更多的训练数据

除此外，我们为了避免overfit，一般都会加正则项。那加了正则项后，新的假设空间会得到一些限制，此时新假设空间的VC维将变小，也就是同样训练数据条件下，Ein更有可能等于Eout，所以泛化能力更强。这里从VC维的角度解释了正则项的作用。

参考

  • 《台湾国立大学-机器学习基石》第六讲
  • 《台湾国立大学-机器学习基石》第七讲
  • VC维的来龙去脉

配图均来自《台湾国立大学-机器学习基石》

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。

文章目录
  1. 1. VC Bound
    1. 1.1. 证明
    2. 1.2. 计算VC
  2. 2. VC Dimension
    1. 2.1. 定义
    2. 2.2. 物理意义
    3. 2.3. 模型复杂度
    4. 2.4. 采样复杂度
  3. 3. 参考